InSAR基于路径的相位解缠算法

两幅SAR图像经过干涉以后，我们可以获得一幅缠绕相位图像，各像元上的值为对应的干涉相位的主值。根据Nyquist定理，当相邻像元上的相位差小于二时，可以通过积分的算法来恢复相位的真实值。基于路径跟踪的相位解缠算法就是通过积分相邻缠绕相位的差分值来恢复相位的真实值的。假设我们己知在像元上的相位，那么在其它像元r上的相位可以通过以下公式来获得:

                                           （4.1）

符号为像元r上的解缠相位，为像元上的已知解缠相位，C为积分路径，根据积分理论：

                                                 （4.2）

上式为积分函数，C为积分路径，（4.2）的线性积分不仅依赖于积分路径C的起点和终点，还依赖于积分路径C本身。要使积分与路径无关，则要求一下闭合积分成立

                                                （4.3）

在二维相位解缠中，公式(4.3)常用来作为探测积分是否与路径无关的条件。InSAR缠绕相位数据中，不是所有的积分路径都满足公式(4.3)，有些像元上的缠绕相位数据由于受到噪声的影响，或者由于其它的原因，导致通过这些像元的闭合积分不能满足公式(4.3)，这些像元上的相位在InSAR中被称为“残差点(residue)”，或者“电荷”(具有正负性，见随后的讨论)，在路径跟踪的相位解缠算法中，关键的问题在于如何判断这些电荷并将它们相连(称为“分枝”)以达到正负抵消，且防止积分路径穿过这些分枝。

路径跟踪法的基本策略是将可能的误差传递限制在噪声区内，通过选择合适的积分路径，隔绝噪声区，阻止相位误差的全程传递。几十年来，研究者研究出了许多的相位解缠算法，至今为止，基于路径跟踪的相位解缠算法有枝切法、区域法、Mask-cut算法、像元扩散法、最小生成树法、条纹检测法、区域生长法，最小不连续算法 (简称Rynn算法)等算法。

路径跟踪的相位解缠算法一般步骤如下所示:

输入:缠绕相位

步骤1:相位连续性/不连续性检测:识别残差点，生成枝切线。

步骤2:计算/建立相位质量图。

步骤3:相位积分:在枝切线周围或在质量图的指导下处理。

下面对其中比较典型的算法作详细介绍:

4.2.1Goldstein枝切法

Goldstein枝切法是较经典的路径跟踪法，是1988年Goldstein等人提出的，它识别正负残差点，并连接邻近的残差点对或多个残差点，实现残差点“电荷”平衡，生成最优的枝切线，确定积分路径，防止误差沿积分路径传递。基本步骤为:

(l)识别残差点;

(2)生成枝切线;

(3)绕过枝切线进行积分。

具体如下:首先按一定的顺序寻找残差点，定义一个2x2像元的缠绕相位为节点，将四个像元串接起来，即为影像中的最小闭合路径 (dosedloop)。沿最小闭合路径将缠绕相位梯度累加起来，如果之和为零则这四个点是一致的，否则左上角的像元就称为残差点(residual)。缠绕相位节点图与最小闭合路径图如图所示:

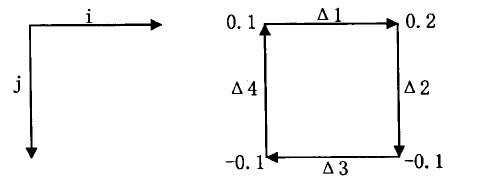
缠绕相位节点，最小闭合路径图(每个像元数值乘以劫才表示缠绕相位真实值)，为各方向相位差:

计算得

说明相位是一致的。再给出一个例子：

缠绕相位节点图与最小闭合路径图如图所示:

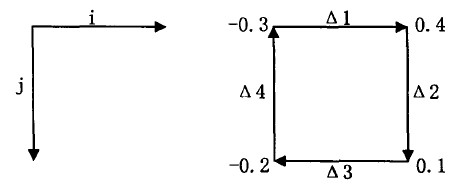
则左上角的像元为残差点，当找到第一个残差点以后，从该残差点开始，继续搜索，找到下一个残差点后，用一枝切线将两者连接起来计算残数和，如果和为零则完成了该树枝的生长，继续搜索直至搜索完全部残差点，如果和不为零则不断加入残差点每次计算总的残数和，直至和为零。

在Goldstein的枝切法中，有两个步骤是极为关键的:(l)当搜索窗口找到新的残差点，无论该残差点是否与其他的残差点相连，都将该残差点与窗口中心的残差点相连;(2)当搜索窗口到达图像的边界，则将残差点与边界相连，以阻止积分路径。

枝切法最大的优点是:在实际计算中速度比较快;在噪声比较低、残差点比较少的情况下，精确度非常高。缺点是:当残差点较多且分布较密集时，该算法难以准确连接枝切线，导致无法选择合理的积分路径，有时会造成错误的阮跳跃，导致误差的传递。但由于该算法的速度优势，使之成为一种常用的相位解缠算法。

2质量引导法

这种算法不识别残差点，也不设置枝切线。而是在进行相位解缠时，通过相位质量图 (quality map)来定义相位数据的质量，将积分路径总是沿“高”质量的像元进行，最后解缠“低”质量像元。

质量引导法的关键步骤就是在相位质量图的引导下进行像元扩散，其基本操作过程如下:从高质量像元点出发，检测它的四个邻近像元，对邻近像元进行解缠，将解缠后的像元的邻接像元(未解缠)存储在“邻接列”中，依据相位质量从“邻接列”移出高质量像元进行相位解缠，更新“邻接列”，重复上述步骤直至所有的像元解缠完毕。

质量引导法成功地进行相位解缠的前提是必须有可靠的相位质量图。相位质量图主要有四种:相干图、伪相干图、相位导数变化图、最大相位梯度图、掩模图(mask)。

(1) 相干图
    最常用的质量图是相干图，相干值的高低表明图像不同区域的相干性，是最直观的干涉质量评价图。同时相干系数的变化也表征了在图像获取期间地物的变化情况，所以相干图也用于地物的分类等。

(2) 伪相干图(Pseudo-correlation)
    当无法获得InSAR图像对的强度值时，常常用伪相干图来模拟相干图。这时把InSAR图像对的强度定义为1，那么伪相干定义为：

k为视数。伪相干图的一个最大缺陷是：对于陡峭地形区，它标志为低质量数据区(即使这些相位数据质量很好，并且没有噪声)。这时就需要新的质量图，用来评价相位导数的统计变化特征。

(3) 相位导数变化图 (Phase Derivative Variance)
    相位导数变化定义如下:

    相位导数变化不同于相干和伪相干。例如，在倾斜地表，如果相位变化率保持一定，则相位导数变化为0，而伪相干不为0。从严格意义上讲，相位导数变化表征的是相位数据的“坏”(badness)，而不是“好”(goodness)，但我们可以假定:如果相位导数变化是可以忽略的话，那么相位数据就是好数据。实验表明，在无法获得相干图的情况下，相位导数变化图是最可靠的相位质量图。

(4) 最大相位梯度图
    从相位图上可以看出，在噪声相位区往往相位梯度也很大，所以可以用最大相位梯度来表征相位数据的质量。一般最大梯度定义为：
     

最大相位梯度图也有伪相干的缺陷，在地形很陡峭(即相位变化显著，但无噪声)也表征为低质量数据。

质量引导法完全依赖于质量图像来指导解缠路径的选择，因此在缺乏高质量的质量图像时，解缠效果将会很不理想。另外该算法不识别残差点，因此解缠路径就不可避免的可能会包围非平衡的残差点，这样就有可能会产生2k二的周期累加错误。

(5) 掩膜图（mask）
    在解缠过程中，有的区域失相关严重(如水面)导致相位不连续，有的区域地势平坦不需要进行滤波。在这种情况下，我们可以制作一个掩模图将这些区域掩盖起来，使解缠和滤波不涉及这些区域。掩模图的生成方法一般是采用一定的闲值来进行判断，或者手工确定需要掩盖的区域，通常被掩盖区域的干涉图像元用0来表示，未被掩盖的像元1来表示。第四章对西安数据的解缠过程中均采用了掩模图，即掩盖掉的像元不参与解缠，以防止误差的传播。
    质量引导法解缠结果的好坏很大程度上依赖于质量图的“好”与“坏”，如果有好的质量图引导，能得到优于枝切法的解缠结果。因为不设置枝切线，积分路径就可能包围残差点导致错误的2kπ的累积错误。

3掩膜切口法（mask-cut法）

1966年Rynn首先对质量图像引导分割路径的算法作了详细的描述，在该方法中使用逐步增长的像素掩模来连接残差点，这种像素掩模称为掩模切口，与分割路径的作用相似。掩模切口算法与质量引导法有些相似，它在有些地方可以看作是后者的逆向算法，它并不是从高质量的区域开始解缠，而是从残差点开始，沿低质量的区域逐渐扩展像素掩模。掩模切口的扩展过程一直到它连接了等量的正残差点和负残差点或者到达图像边界时为止，在前一种情况下，残差点是平衡的，相位解缠与积分路径无关，而在后一种情况下，掩模将残差点隔离开来，可以保证不会有解缠路径可能包围这些残差点。

该算法实际上是将Goldstein枝切法和基于质量图路径积分法的结合起来，掩模分害」算法虽然也识别残差点并产生分割路径，但总的来讲，该算法还是在质量图像的指导下实现的，因此算法的结果在很大程度上也仍然依赖于高质量的质量图像。在残留点不仅仅分布在低质量相位区的情况下，mask-cut算法与质量指导的路径跟踪算法都无法正常工作，在这种情况下，枝切法更为有效。

其解缠步骤为:

(l)识别残差点；

(2)生成mask-cut；

(3)细化mask-cut；

(4)沿mask-cut的路径积分。